Which Aspect Of Your Drawing Is Due To Double Slit Interference

215 27.3 Young's Double Slit Experiment

Summary

• Explicate the phenomena of interference.
• Define constructive interference for a double slit and destructive interference for a double slit.

Although Christiaan Huygens thought that low-cal was a wave, Isaac Newton did not. Newton felt that in that location were other explanations for color, and for the interference and diffraction furnishings that were observable at the time. Attributable to Newton's tremendous stature, his view by and large prevailed. The fact that Huygens's principle worked was not considered prove that was straight enough to show that light is a wave. The credence of the wave graphic symbol of light came many years later when, in 1801, the English physicist and doc Thomas Young (1773–1829) did his now-classic double slit experiment (encounter Figure 1).

Effigy ane. Young'south double slit experiment. Here pure-wavelength light sent through a pair of vertical slits is diffracted into a pattern on the screen of numerous vertical lines spread out horizontally. Without diffraction and interference, the low-cal would just make two lines on the screen.

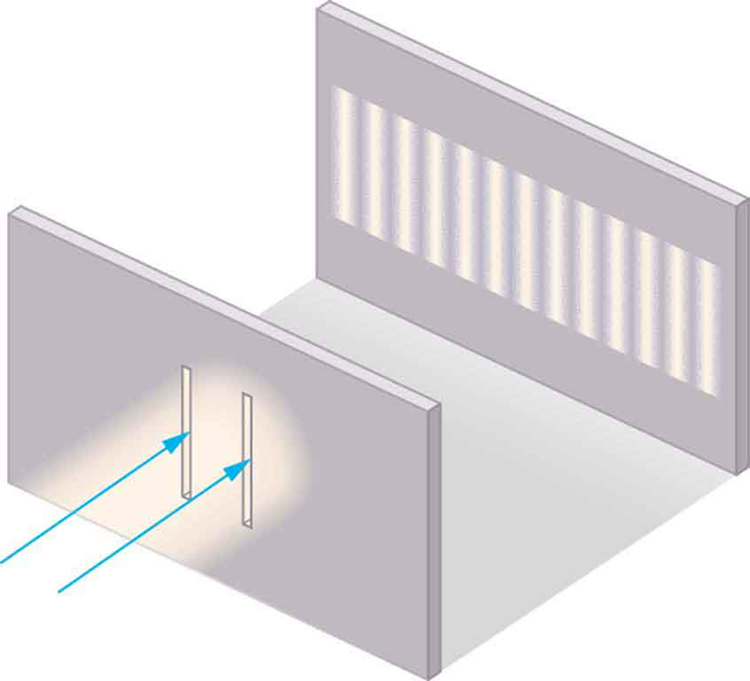
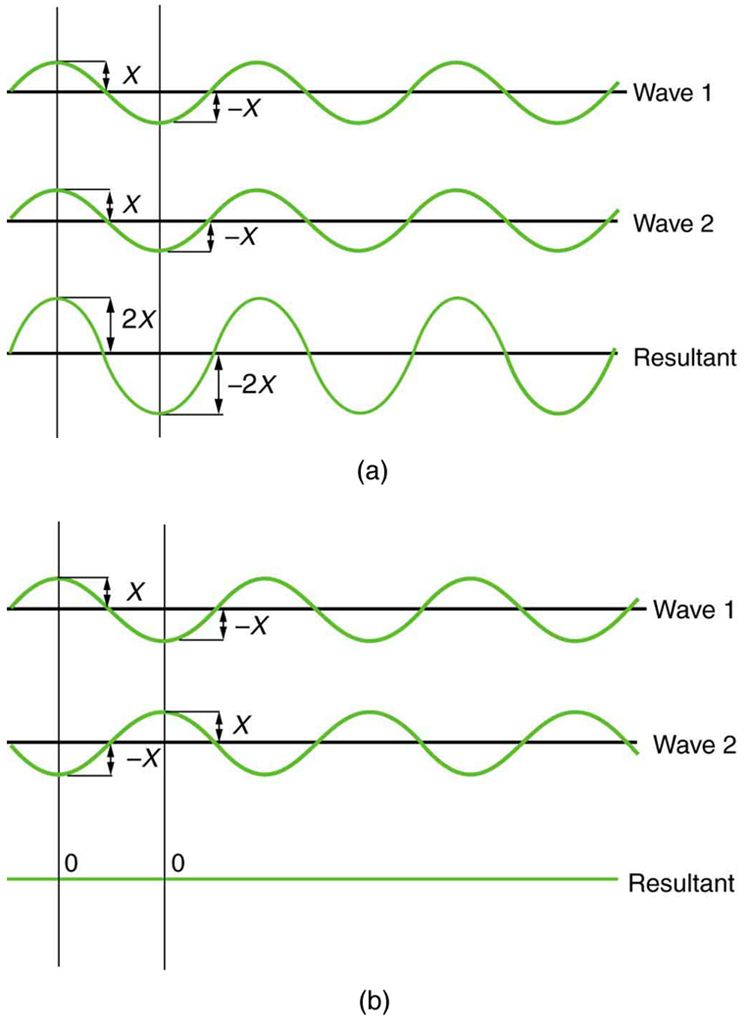
Why do we not commonly observe wave behavior for calorie-free, such as observed in Young'due south double slit experiment? Offset, lite must interact with something small, such as the closely spaced slits used by Young, to show pronounced moving ridge effects. Furthermore, Young first passed light from a single source (the Sun) through a single slit to make the light somewhat coherent. Past coherent, we mean waves are in phase or accept a definite phase relationship. Incoherent means the waves have random phase relationships. Why did Young then pass the light through a double slit? The reply to this question is that two slits provide ii coherent light sources that then interfere constructively or destructively. Young used sunlight, where each wavelength forms its own design, making the upshot more than difficult to see. We illustrate the double slit experiment with monochromatic (single [latex]\boldsymbol{\lambda}[/latex]) light to analyze the outcome. Figure 2 shows the pure constructive and destructive interference of ii waves having the same wavelength and aamplitude.

Figure 2. The amplitudes of waves add. (a) Pure constructive interference is obtained when identical waves are in phase. (b) Pure destructive interference occurs when identical waves are exactly out of stage, or shifted by half a wavelength.

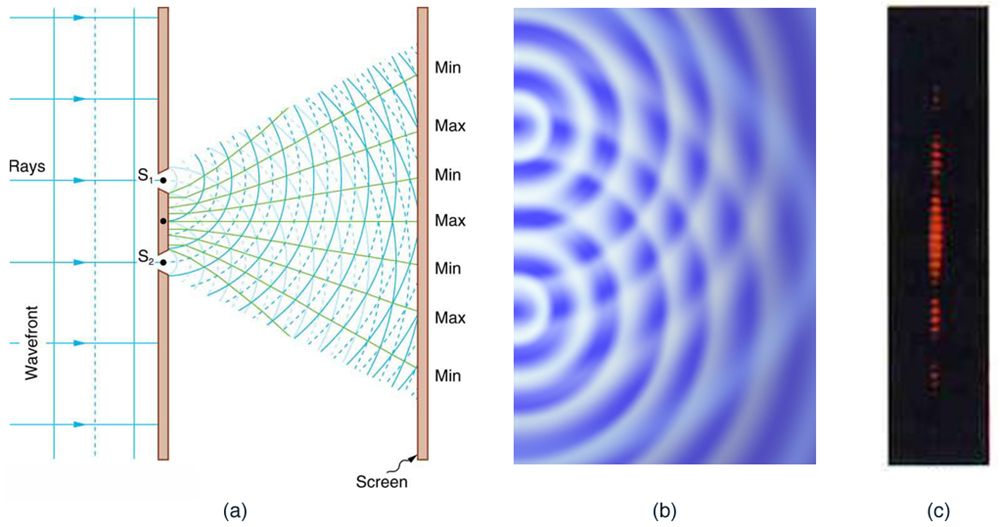
When light passes through narrow slits, information technology is diffracted into semicircular waves, as shown in Figure 3(a). Pure constructive interference occurs where the waves are crest to crest or trough to trough. Pure subversive interference occurs where they are crest to trough. The light must fall on a screen and be scattered into our eyes for us to run across the pattern. An analogous blueprint for water waves is shown in Figure 3(b). Note that regions of constructive and destructive interference movement out from the slits at well-defined angles to the original beam. These angles depend on wavelength and the distance between the slits, every bit we shall meet below.

Figure three. Double slits produce two coherent sources of waves that interfere. (a) Light spreads out (diffracts) from each slit, because the slits are narrow. These waves overlap and interfere constructively (bright lines) and destructively (nighttime regions). Nosotros can only see this if the light falls onto a screen and is scattered into our eyes. (b) Double slit interference design for water waves are nearly identical to that for light. Wave action is greatest in regions of constructive interference and least in regions of destructive interference. (c) When calorie-free that has passed through double slits falls on a screen, nosotros encounter a pattern such equally this. (credit: PASCO)

To understand the double slit interference design, nosotros consider how ii waves travel from the slits to the screen, as illustrated in Figure four. Each slit is a different altitude from a given point on the screen. Thus different numbers of wavelengths fit into each path. Waves outset out from the slits in phase (crest to crest), merely they may stop upwardly out of phase (crest to trough) at the screen if the paths differ in length by half a wavelength, interfering destructively equally shown in Figure four(a). If the paths differ by a whole wavelength, then the waves get in in stage (crest to crest) at the screen, interfering constructively as shown in Figure 4(b). More mostly, if the paths taken past the two waves differ by whatsoever half-integral number of wavelengths [[latex]\boldsymbol{(1/2) \;\lambda}[/latex], [latex]\boldsymbol{(3/2) \;\lambda}[/latex], [latex]\boldsymbol{(v/2) \;\lambda}[/latex], etc.], then subversive interference occurs. Similarly, if the paths taken by the two waves differ by any integral number of wavelengths ([latex]\boldsymbol{\lambda}[/latex], [latex]\boldsymbol{2 \lambda}[/latex], [latex]\boldsymbol{three \lambda}[/latex], etc.), and so constructive interference occurs.

Have-Home Experiment: Using Fingers every bit Slits

Look at a low-cal, such equally a street lamp or incandescent bulb, through the narrow gap between two fingers held close together. What type of design do you encounter? How does it change when you let the fingers to motility a little farther autonomously? Is it more distinct for a monochromatic source, such as the yellow light from a sodium vapor lamp, than for an incandescent bulb?

Figure 4. Waves follow different paths from the slits to a common signal on a screen. (a) Destructive interference occurs hither, because one path is a half wavelength longer than the other. The waves outset in phase but arrive out of stage. (b) Constructive interference occurs hither because 1 path is a whole wavelength longer than the other. The waves offset out and arrive in stage.

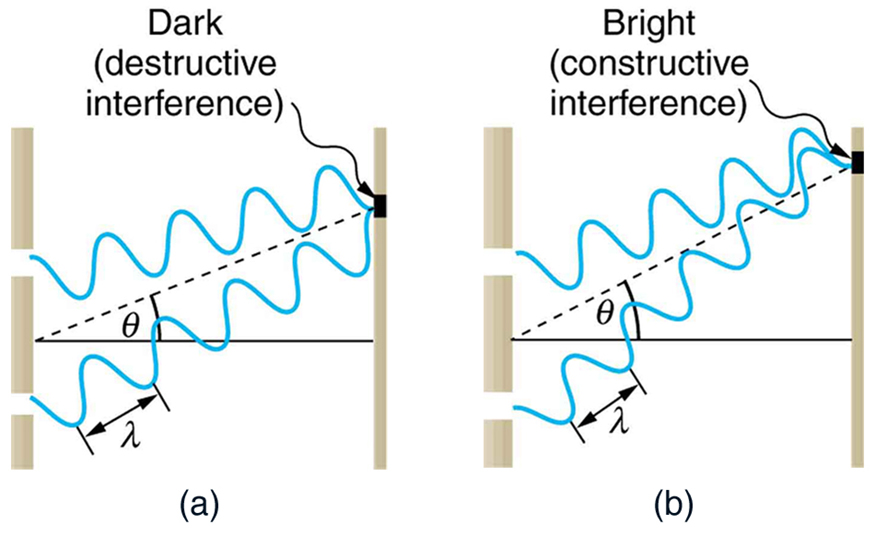
Figure 5 shows how to determine the path length divergence for waves traveling from ii slits to a common indicate on a screen. If the screen is a large distance away compared with the altitude between the slits, then the angle [latex]\boldsymbol{\theta}[/latex] between the path and a line from the slits to the screen (meet the figure) is nearly the same for each path. The difference between the paths is shown in the figure; simple trigonometry shows it to be [latex]\boldsymbol{d \;\textbf{sin} \;\theta}[/latex], where [latex]\boldsymbol{d}[/latex] is the distance between the slits. To obtain constructive interference for a double slit, the path length deviation must be an integral multiple of the wavelength, or

[latex]\boldsymbol{d \;\textbf{sin} \;\theta = grand \lambda, \;\textbf{for} \; one thousand = 0, \; 1, \; -ane, \; 2, \; -ii,\; \dots \;\;\;(\textbf{constructive})}.[/latex]

Similarly, to obtain destructive interference for a double slit, the path length difference must exist a one-half-integral multiple of the wavelength, or

[latex]\boldsymbol{d \;\textbf{sin} \;\theta = m +}[/latex][latex]\boldsymbol{\frac{1}{ii}}[/latex][latex]\boldsymbol{\lambda , \;\textbf{for} \; 1000 = 0, \; 1, \; -i, \; 2, \; -2, \dots \;\;\; (\textbf{destructive})}[/latex]

where [latex]\boldsymbol{\lambda}[/latex] is the wavelength of the low-cal, [latex]\boldsymbol{d}[/latex] is the distance betwixt slits, and [latex]\boldsymbol{\theta}[/latex] is the bending from the original direction of the axle every bit discussed above. We call [latex]\boldsymbol{m}[/latex] the order of the interference. For example, [latex]\boldsymbol{g = 4}[/latex] is fourth-order interference.

Effigy 5. The paths from each slit to a common betoken on the screen differ by an amount d sin θ , assuming the distance to the screen is much greater than the distance between slits (non to scale here).

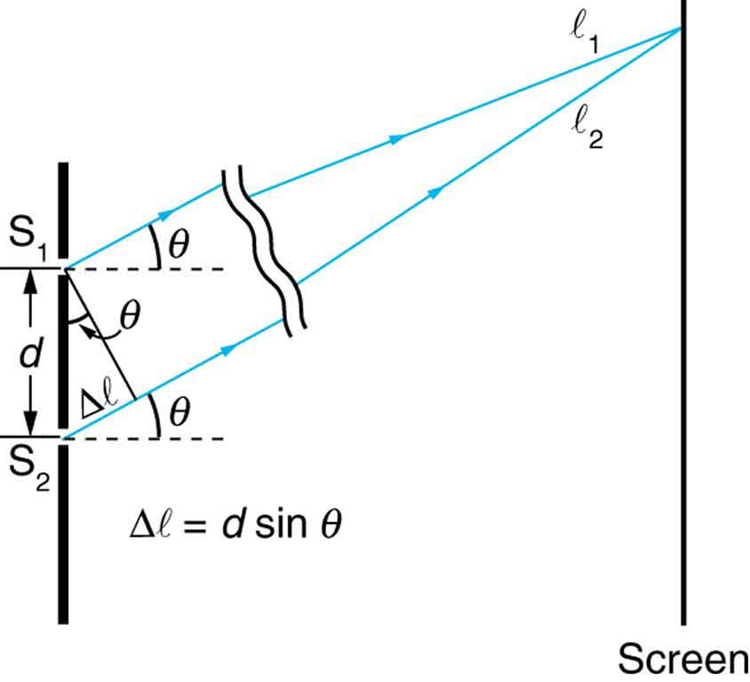
The equations for double slit interference imply that a series of bright and dark lines are formed. For vertical slits, the calorie-free spreads out horizontally on either side of the incident beam into a pattern chosen interference fringes, illustrated in Effigy vi. The intensity of the brilliant fringes falls off on either side, being brightest at the center. The closer the slits are, the more is the spreading of the bright fringes. We can see this by examining the equation

[latex]\boldsymbol{d \;\textbf{sin} \;\theta = m \theta , \;\textbf{for} \; m = 0, \;ane, \; -1, \; 2, \; -ii, \; \dots}.[/latex]

For fixed [latex]\boldsymbol{\lambda}[/latex] and [latex]\boldsymbol{m}[/latex], the smaller [latex]\boldsymbol{d}[/latex] is, the larger [latex]\boldsymbol{\theta}[/latex] must be, since [latex]\boldsymbol{\textbf{sin} \;\theta = yard \lambda / d}[/latex].

This is consistent with our contention that wave effects are most noticeable when the object the wave encounters (here, slits a altitude [latex]\boldsymbol{d}[/latex] apart) is pocket-sized. Minor [latex]\boldsymbol{d}[/latex] gives large [latex]\boldsymbol{\theta}[/latex], hence a large issue.

Figure half-dozen. The interference design for a double slit has an intensity that falls off with angle. The photograph shows multiple vivid and dark lines, or fringes, formed by calorie-free passing through a double slit.

Case 1: Finding a Wavelength from an Interference Design

Suppose you pass light from a He-Ne laser through 2 slits separated by 0.0100 mm and find that the tertiary bright line on a screen is formed at an angle of [latex]\boldsymbol{10.95 ^{\circ}}[/latex] relative to the incident beam. What is the wavelength of the low-cal?

Strategy

The third bright line is due to third-society constructive interference, which ways that [latex]\boldsymbol{chiliad = three}[/latex]. We are given [latex]\boldsymbol{d = 0.0100 \;\textbf{mm}}[/latex] and [latex]\boldsymbol{\theta = 10.95^{\circ}}[/latex]. The wavelength can thus exist found using the equation [latex]\boldsymbol{d \;\textbf{sin} \;\theta = m \lambda}[/latex] for constructive interference.

Solution

The equation is [latex]\boldsymbol{d \;\textbf{sin} \;\theta = one thousand \lambda}[/latex]. Solving for the wavelength [latex]\boldsymbol{\lambda}[/latex] gives

[latex]\boldsymbol{\lambda =}[/latex][latex]\boldsymbol{\frac{d \;\textbf{sin} \;\theta}{yard}}.[/latex]

Substituting known values yields

[latex]\brainstorm{array}{r @{{}={}}l} \boldsymbol{\lambda} & \boldsymbol{\frac{(0.0100 \;\textbf{mm})(\textbf{sin} 10.95^{\circ})}{iii}} \\[1em] & \boldsymbol{6.33 \times ten^{-4} \;\textbf{mm} = 633 \;\textbf{nm}}. \end{array}[/latex]

Discussion

To three digits, this is the wavelength of light emitted by the common He-Ne laser. Not past coincidence, this ruby colour is similar to that emitted by neon lights. More important, however, is the fact that interference patterns can exist used to measure out wavelength. Young did this for visible wavelengths. This analytical technique is yet widely used to measure electromagnetic spectra. For a given guild, the bending for constructive interference increases with [latex]\boldsymbol{\lambda}[/latex], so that spectra (measurements of intensity versus wavelength) can be obtained.

Example 2: Computing Highest Social club Possible

Interference patterns do not have an space number of lines, since there is a limit to how big [latex]\boldsymbol{m}[/latex] can be. What is the highest-order constructive interference possible with the organization described in the preceding example?

Strategy and Concept

The equation [latex]\boldsymbol{d \;\textbf{sin} \;\theta = m \lambda \; (\textbf{for} \; m = 0, \; 1, \; -one, \; ii, \; -2, \; \dots)}[/latex] describes effective interference. For fixed values of [latex]\boldsymbol{d}[/latex] and [latex]\boldsymbol{\lambda}[/latex], the larger [latex]\boldsymbol{one thousand}[/latex] is, the larger [latex]\boldsymbol{\textbf{sin} \;\theta}[/latex] is. Notwithstanding, the maximum value that [latex]\boldsymbol{\textbf{sin} \;\theta}[/latex] tin can take is 1, for an angle of [latex]\boldsymbol{90 ^{\circ}}[/latex]. (Larger angles imply that light goes astern and does non reach the screen at all.) Let u.s. find which [latex]\boldsymbol{m}[/latex] corresponds to this maximum diffraction angle.

Solution

Solving the equation [latex]\boldsymbol{d \;\textbf{sin} \;\theta = one thousand \lambda}[/latex] for [latex]\boldsymbol{yard}[/latex] gives

[latex]\boldsymbol{m =}[/latex][latex]\boldsymbol{\frac{d \;\textbf{sin} \;\theta}{\lambda}}.[/latex]

Taking [latex]\boldsymbol{\textbf{sin} \;\theta = 1}[/latex] and substituting the values of [latex]\boldsymbol{d}[/latex] and [latex]\boldsymbol{\lambda}[/latex] from the preceding example gives

[latex]\boldsymbol{m =}[/latex][latex]\boldsymbol{\frac{(0.0100 \;\textbf{mm})(1)}{633 \;\textbf{nm}}}[/latex][latex]\boldsymbol{\approx fifteen.8}.[/latex]

Therefore, the largest integer [latex]\boldsymbol{m}[/latex] can be is xv, or

[latex]\boldsymbol{m = 15}.[/latex]

Discussion

The number of fringes depends on the wavelength and slit separation. The number of fringes volition exist very large for large slit separations. However, if the slit separation becomes much greater than the wavelength, the intensity of the interference pattern changes so that the screen has ii bright lines bandage past the slits, as expected when light behaves like a ray. We also note that the fringes go fainter farther away from the middle. Consequently, non all 15 fringes may be observable.

Section Summary

• Young's double slit experiment gave definitive proof of the moving ridge grapheme of calorie-free.
• An interference pattern is obtained past the superposition of light from 2 slits.
• There is constructive interference when [latex]\boldsymbol{d \;\textbf{sin} \;\theta = m \lambda \;(\textbf{for} \; g = 0, \; 1, \; -1, \;ii, \; -two, \dots)}[/latex], where [latex]\boldsymbol{d}[/latex] is the distance between the slits, [latex]\boldsymbol{\theta}[/latex] is the angle relative to the incident direction, and [latex]\boldsymbol{m}[/latex] is the order of the interference.
• There is destructive interference when [latex]\boldsymbol{d \;\textbf{sin} \;\theta = (thousand+ \frac{1}{two}) \lambda}[/latex] (for [latex]\boldsymbol{grand = 0, \; 1, \; -1, \; 2, \; -2, \; \dots}[/latex]).

Conceptual Questions

1: Young's double slit experiment breaks a single light beam into two sources. Would the same design exist obtained for two independent sources of low-cal, such as the headlights of a afar car? Explicate.

2: Suppose you use the aforementioned double slit to perform Immature's double slit experiment in air and and so echo the experiment in water. Do the angles to the same parts of the interference design go larger or smaller? Does the color of the light change? Explain.

3: Is information technology possible to create a situation in which there is just destructive interference? Explicate.

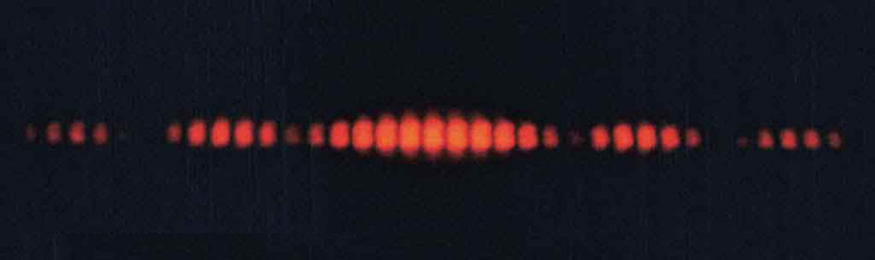
four: Figure 7 shows the key part of the interference pattern for a pure wavelength of red light projected onto a double slit. The pattern is actually a combination of single slit and double slit interference. Note that the bright spots are evenly spaced. Is this a double slit or single slit characteristic? Notation that some of the brilliant spots are dim on either side of the center. Is this a single slit or double slit characteristic? Which is smaller, the slit width or the separation betwixt slits? Explain your responses.

Figure 7. This double slit interference pattern also shows signs of single slit interference. (credit: PASCO)

Problems & Exercises

1: At what angle is the first-order maximum for 450-nm wavelength blue low-cal falling on double slits separated by 0.0500 mm?

2: Calculate the bending for the third-guild maximum of 580-nm wavelength yellow light falling on double slits separated past 0.100 mm.

three: What is the separation between two slits for which 610-nm orangish light has its start maximum at an angle of [latex]\boldsymbol{30.0 ^{\circ}}[/latex]?

4: Find the distance between two slits that produces the outset minimum for 410-nm violet lite at an angle of [latex]\boldsymbol{45.0 ^{\circ}}[/latex].

5: Calculate the wavelength of light that has its third minimum at an angle of [latex]\boldsymbol{30.0 ^{\circ}}[/latex] when falling on double slits separated past [latex]\boldsymbol{three.00 \;\mu \textbf{one thousand}}[/latex]. Explicitly, bear witness how you follow the steps in Chapter 27.vii Problem-Solving Strategies for Moving ridge Optics.

half-dozen: What is the wavelength of lite falling on double slits separated past [latex]\boldsymbol{2.00 \;\mu \textbf{m}}[/latex] if the third-society maximum is at an angle of [latex]\boldsymbol{threescore.0 ^{\circ}}[/latex]?

7: At what angle is the fourth-order maximum for the situation in Problems & Exercises 1?

8: What is the highest-order maximum for 400-nm light falling on double slits separated by [latex]\boldsymbol{25.0 \;\mu \textbf{m}}[/latex]?

ix: Find the largest wavelength of light falling on double slits separated by [latex]\boldsymbol{1.20 \;\mu \textbf{1000}}[/latex] for which at that place is a first-order maximum. Is this in the visible part of the spectrum?

10: What is the smallest separation betwixt two slits that will produce a second-order maximum for 720-nm red lite?

11: (a) What is the smallest separation between two slits that will produce a second-guild maximum for whatsoever visible low-cal? (b) For all visible light?

12: (a) If the first-order maximum for pure-wavelength light falling on a double slit is at an angle of [latex]\boldsymbol{10.0^{\circ}}[/latex], at what angle is the 2nd-order maximum? (b) What is the angle of the first minimum? (c) What is the highest-lodge maximum possible hither?

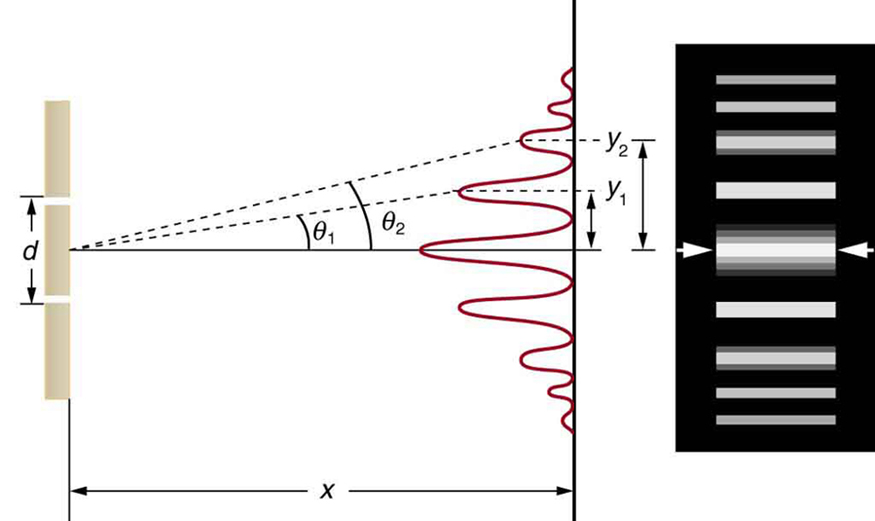
13: Figure 8 shows a double slit located a distance [latex]\boldsymbol{ten}[/latex] from a screen, with the altitude from the eye of the screen given past [latex]\boldsymbol{y}[/latex]. When the altitude [latex]\boldsymbol{d}[/latex] betwixt the slits is relatively large, there will exist numerous bright spots, called fringes. Show that, for pocket-size angles (where [latex]\boldsymbol{\textbf{sin} \;\theta \approx \theta}[/latex], with [latex]\boldsymbol{\theta}[/latex] in radians), the distance between fringes is given by [latex]\boldsymbol{\Delta y = ten \lambda /d}[/latex].

Figure viii. The distance between adjacent fringes is Δy = xλ/d , bold the slit separation d is large compared with λ .

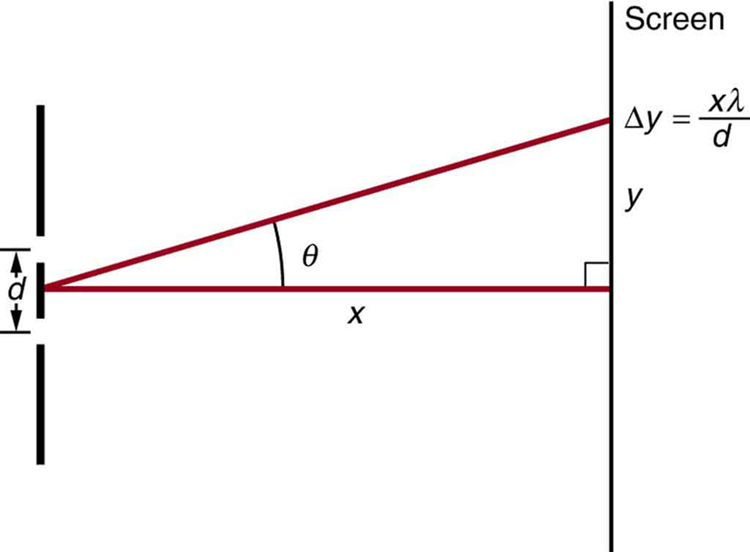
14: Using the result of the problem above, calculate the distance between fringes for 633-nm calorie-free falling on double slits separated by 0.0800 mm, located iii.00 m from a screen every bit in Effigy eight.

15: Using the result of the trouble 2 bug prior, find the wavelength of light that produces fringes 7.fifty mm autonomously on a screen ii.00 one thousand from double slits separated past 0.120 mm (meet Effigy 8).

Glossary

coherent

waves are in phase or have a definite phase human relationship

constructive interference for a double slit

the path length difference must be an integral multiple of the wavelength

destructive interference for a double slit

the path length divergence must exist a half-integral multiple of the wavelength

incoherent

waves have random phase relationships

society

the integer [latex]\boldsymbol{k}[/latex] used in the equations for constructive and destructive interference for a double slit

Solutions

Problems & Exercises

1: [latex]\boldsymbol{0.516 ^{\circ}}[/latex]

three: [latex]\boldsymbol{1.22 \times 10^{-vi} \;\textbf{m}}[/latex]

5: 600 nm

7: [latex]\boldsymbol{2.06 ^{\circ}}[/latex]

9: 1200 nm (not visible)

xi: (a) 760 nm

(b) 1520 nm

13: For modest angles [latex]\boldsymbol{\textbf{sin} \;\theta - \;\textbf{tan} \;\theta \approx \theta}[/latex] (in radians).

For two adjacent fringes we accept,

[latex]\boldsymbol{d \;\textbf{sin} \;\theta _{\textbf{yard}} = m \lambda}[/latex]

and

[latex]\boldsymbol{d \;\textbf{sin} \;\theta _{\textbf{m}+1} = (m+1) \lambda}[/latex]

Subtracting these equations gives

[latex]\begin{assortment}{r @{{}={}}l} \boldsymbol{d (\textbf{sin} \; \theta _{\textbf{m} + 1} - \textbf{sin} \; \theta _{\textbf{one thousand}})} & \boldsymbol{[(yard + 1) - m] \lambda} \\[1em] \boldsymbol{d(\theta _{{\textbf{m}} + i} - \theta _{\textbf{m}})} & \boldsymbol{\lambda} \cease{array}[/latex]

[latex]\boldsymbol{\textbf{tan} \;\theta _{\textbf{thousand}} = \frac{y_{\textbf{m}}}{x} \approx \theta _{\textbf{thousand}} \Rightarrow d(\frac{y_{\textbf{thousand}+1}}{x}- \frac{y_{\textbf{m}}}{x}) = \lambda}[/latex]

[latex]\boldsymbol{d \frac{\Delta y}{ten} = \lambda \Rightarrow \Delta y = \frac{ten \lambda}{d}}[/latex]

15: 450 nm

Source: https://iu.pressbooks.pub/openstaxcollegephysics/chapter/youngs-double-slit-experiment/

Posted by: fostersagoonger.blogspot.com

Share this post